Квантовая механика и вакуум.

 

 

Вступление

 

 

В  конце  20-х  годов  нашего  тысячелетия  были  созданы  квантовая  механика,  квантовая  электродинамика  и  квантовая  теория  поля,  приведшие  теорию  и  практику  к  поразительней­шим  результатам  [1].

Квантовая  теория  поля,  для  описания  универсальной  вза­имной   превращаемости   частиц,   вводит  квантовое  волновое  поле – f (r, t), т.е.  построение  квантовой  теории  систем  с  беско­нечным  числом  степеней  свободы.  Этот  переход  объясняется  с  помощью  следующей  аналогии:  представим  себе,  что  всё  про­странство  заполнено  связанными  между  собой  гармоническими  осцилляторами.  Получившееся  поле  осцилляторов,  очевидно,  имеет  бесконечно  большое  количество  степеней  свободы.  В  рас­сматриваемой  системе  могут  распространяться  волны  колебаний  этих  связанных  между  собой  осцилляторов.

При  переходе  к  квантовой  механике  классическая  вели­чина,  характеризующая  каждый  осциллятор,  становиться  опера­торами,  а  с  каждой  волной  сопоставляется  частица,  обладающая  такими  же,  как  и  волна,  энергией  и  импульсом,  а  следовательно  и  массой.  Эту  частицу  нельзя  отождествить  ни  с  одним  из  ос­цилляторов  поля  в  отдельности:  она  представляет  собой  резуль­тат  процесса,  захватывающего  бесконечно  большое  число  осцил­ляторов  и  описывает  некое  возбуждение  поля.

Т.о.  изучение  поля  можно  свести  к  рассмотрению  кванто­вых  волн  (или  частиц)  возбуждений,  их  рождения  и  поглоще­ния.  Но  для  дальнейшего  рассуждения  нам  необходима  лишь  сама  идея  о  заполненности  всего  пространства  связанными  ме­жду  собой  гармоническими  осцилляторами.

 

 

Часть I

 

Электрон-позитронная пара, как кандидат на звание осциллятора.

 

         В этой небольшой части рассмотрим вопрос аннигиляции электрон – позитронных пар, в частности позитрония. Т.е. рассмотрим реакцию вида:

 

 

Исходя из размеров позитрония примерно равных удвоенному размеру атома водорода (Физический энциклопедический словарь, Москва, “Большая Российская энциклопедия” 1995 г. статья Позитроний), определим энергию электростатического взаимодействия:

 

 

 

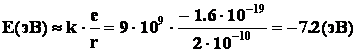
где  k = 1/4πε_о – постоянная электростатического взаимодействия;

        е – заряд электрона.

 

            Как было показано в предыдущей работе – “Есть ли электроны в атомном ядре?  Есть!!!”– электроны могут существовать внутри нуклонов (по крайней мере, этому ничто не препятствует) и, следовательно, размеры электрона сравнимы с размерами нуклонов (а если точнее, то намного меньше).

Частицы, в нашем случае электрон и позитрон, под действием электростатического поля приобретают кинетическую энергию. Расстояние – R, на котором электрон и позитрон приобретут кинетическую энергию равную их энергии покоя (К=1,022 МэВ), равно:

 

 

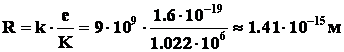
Допустим, что этот момент и является моментом “аннигиляции”. Баланс энергии на этом расстоянии выглядит следующим образом:

 

 

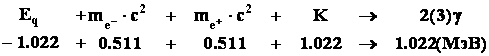
В данном случае мы не учитывали первоначальную энергию электростатического взаимодействия, считая ее пренебрежимо малой (1,022 Мэв>>7.2эВ).

Исходя из того, что излучать эл/магнитные волны могут только ускоренно движущиеся заряды, следует, что на излучение двух либо трех γ – квантов “расходуется” кинетическая энергия. А так же из того, что под действием γ – квантов (Е ≥1,022 МэВ) в кулоновском поле тяжелых частиц возможно “рождение” электрон – позитронных пар, следует предположение о том, что:

Потеряв скорость, электрон и позитрон образуют связанную пару с массой, стремящейся (равной) к нулю, что обусловлено дефектом масс из-за энергии связи (аналогично объяснению потери массы при образовании дейтрона из двух протонов).

Такая система, в виде электрон – позитронной пары в связанном состоянии, способна изменять свои размеры в ответ на  внешнее эл/магнитное воздействие, стремясь при этом ослабить его, т.о. она вполне соответствует квантовому осциллятору.

Но для того, чтобы такой электрон – позитронный осциллятор существовал, необходимы силы, которые остановят полную аннигиляцию.

Следовательно, существует более высокий вакуум, назовем его  вакуум 2–го  рода, который так же обладает какой – то периодической структурой, благодаря которой возможно появление сил отталкивания двух зарядов противоположного знака.

Эти же силы не дадут возможности аннигиляции двух соседних пар и, следовательно, отвечают за возникновение упорядоченной, псевдо-кристаллической структуры нашего вакуума (вакуума 1-го рода).

Хотя невозбужденный вакуум в целом нейтрален, в нем возможна самопроизвольная,  спонтанная поляризация. Вследствии чего, он (вакуум) должен обладать некоторой доменоподобной структурой, которая  разрушается при наложении внешнего поля или внесении свободного заряда. Кроме того, при внесении в такую систему массы, а тем более заряженной частицы, обладающей массой, плотность электрон-позитронных осцилляторов увеличивается, расстояние между ними уменьшаются.

Вывод: Вакуум заполнен электрон – позитронными парами в связанном состоянии,

его структура – аналогична структуре диэлектрика, изучение свойств которого объяснит очень многое, включая волновые свойства частиц, квантовые свойства атомов и их ядер. Позволит разобраться со структурой “элементарных” частиц, которую возможно будет представить в виде различных комбинаций электронов либо позитронов и их пар, объяснит “холодный” ядерный синтез и условия его оптимального протекания.

 

Часть II.

 

Вакуум  и  КМ.

 

Предположим, что расположение  электрон – позитронных осцилляторов     в  пространстве   опре­деляется   кубической  структурой. Т.е. фактически мы  задаем  диэлектрик  с  определенными  параметрами,  в  который   необходимо  поместить заряд  и   рассмотреть,   что  в   нем   происходит.

Расположим  в  узле   решетки   нескомпенсированный  заряд, этот  заряд  вызовет  поляризацию  диэлектрика.

Рассмотрим  поле  в  точке  пространства B на  расстоянии  r  от  центрального   заряда,  где 

 

Взаимодействие  происходит  не  только  с  центральным  зарядом, но  и  с  окружающими  эту  точку  осцилляторами,   тогда

 

где i, k, n –  целые числа, определяющие координаты осцилляторов по осям x,y,z.

      –  суммирование  по  всем   возможным   значениям  координат осцилляторов

       изменяющихся от  - ∞  до  ∞

 

где

                                              

 

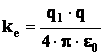
Считая, что тангенциальная составляющая воздействия осцилляторов взаимокомпенсируется, рассчитаем  воздействие  осциллятора О на  произвольную  точку  пространства В (Фиг.1)

 

 

где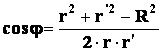      

r’ – расстояние между точкой воздействия и осциллятором;

R– расстояние от начала координат до осциллятора.

            i, k, n –  целые числа, определяющие координаты осцилляторов по осям x,y,z.

 

Все  расстояния выражены  в  относительных  единицах длины, т.е. разделены на d₁(≈10^-15÷10^-14м)– расстояние между центрами осцилляторов – параметр (размер) вакуумной решетки. Подставляя  значения  в  предыдущую  формулу,  получаем:

 

 

Введем  коэффициент  поляризации  ξ,  для  учета  влияния  центрального  заряда  на  осцилляторы

 

 

h -- коэффициент  смещения, зависит от величины заряда, массы и объема пространства, занимаемого частицей. Для протона он примерно  равен  0,3. При нулевых значениях координат осцилляторов коэффициент поляризации приравняем (для простоты) к коэффициенту смещения, т.к. нулевое значение координат принадлежит свободному заряду.

Т.к.  заряды  смещаются  в  обе  стороны  радиально,  то  изменение  их  положения  будет  описываться  этим  коэффициентом.

Например,  координата  i  будет  изменяться  следующим  образом

 

 

теперь  мы  можем  написать  общую  формулу  для  E_ikn

 

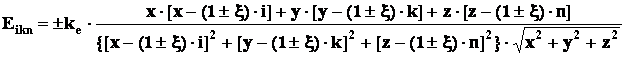
Полная  энергия  взаимодействия  в  любой  точке  пространства  определяется  суммарным  воздействием  центрального  заряда  и  всех  осцилляторов 

 

 

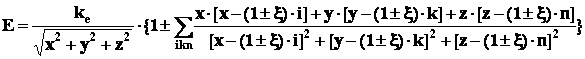
По  этой  формуле  рассчитаем  график  зависимости  потенциальной   энергии  электростатического  взаимодействия  от  расстояния в  пространстве, заполненном осцилляторами (график фиг. 2). Для  упрощения  расчетов примем,  что  частицы  взаимодействуют  вдоль  оси  x,  при  этом  y  и  z равны  нулю.

 

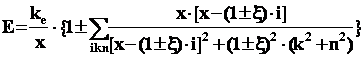   (1)

 

  Полученная  формула,  при  значительных  расстояниях (в  тысячах  i k n),  совпадает  с  общеизвестной (r ≡ x)

 

а  при  меньших  расстояниях,  более  полно  описывает  процессы,  происходящие  в  вакууме.

Расположив свободный, нескомпенсированный заряд между узлами решетки, получим  несколько иное, но очень похожее выражение:

 

  (1’)

 

На  графиках функции (Фиг.2), (3) и (4), построенных для различных значений коэффициента смещения и различными пределами суммирования по i, k, n, четко просматривается  синусоидальная составляющая затухающей амплитуды, возникшая благодаря периодической структуре вакуума. (Примечание: пределы параметров для фиг.2 и 3 i = ± 10; k = n = ± 4; ξ = 0,3; фиг.4 i =  k = n = ± 19; ξ = 0,4)

            Исследуя графики полученных зависимостей, можем выделить несколько интересных зон:

1 – зона от начала координат  до первого нулевого значения энергии – зона внутринуклонного (внутриядерного) отталкивания;

2 – небольшая зона около первого нулевого значения энергии – зона внутринуклонных либо ядерных оболочек (проявляющихся при учете свойств вакуума 2-города);

3 – следующая зона, по протяженности составляющая несколько тысяч d₁, расстояние до следующего нулевого значения энергии – зона притяжения одинаковых по знаку частиц;

4 – зона, непосредственно прилегающая к предыдущей, вблизи нулевого значения энергии – зона электронных атомных оболочек;

5 – далее следует зона “свободных”, несвязанных зарядов.

 

Точность формул в зонах 1 и 2, т.е. при расстояниях r ≤ 2d₁ мала. Все дело в том, что при таких расстояниях между частицами существенное влияние на энергию взаимодействия оказывает уже вакуум 2-го рода, параметры которого нам пока неизвестны.

Зона 3 интересна тем, что она  существует  благодаря, скажем  так, вакуумной экранировке, в ней происходит  притяжение  зарядов  одного  знака  и отталкивание зарядов противоположного  знака. Существование  этой  зоны, например,  великолепно  объясняет, почему в реакции нейтронизации протонов необходимы электроны с энергией более 1,2 МэВ.

А вот анализ  зоны 4 – зоны электронных атомных оболочек, позволяет совершенно по новому взглянуть на физику процессов:

Во – первых становится понятным почему электроны при образовании атома или при изменении орбиты (энергетического уровня) излучают – они попадают в знакопеременное электростатическое поле;

Во – вторых расстояние между соседними разрешенными энергетическими уровнями мало и равно d₁ – параметру вакуумной решетки.

Но этого мало, мы, практически, рассмотрели лишь электростатическое взаимодействие. Элементарная логика требует введения еще одного коэффициента – коэффициента смещения центров осцилляторов при внесении массивного заряда. Это смещение происходит потому, что при поляризации вакуума под действием заряда изменяется взаимодействие между осцилляторами (разрушается доменная структура, устанавливается жесткая ориентация). Гравитационное воздействие массы заряда вызывает “уплотнение” решетки – т.е. так же уменьшает расстояние между осцилляторами.

Предположив  изменение параметра вакуума, а, следовательно, и  координат осцилляторов  в виде экспоненциальной зависимости типа:

 

где γ – коэффициент смещения осцилляторов;

      R –  как и раньше, расстояние от центрального  заряда до осциллятора;

      r_q– размеры частицы.

Получим несколько видоизмененные формулы (1) и (1’):

 

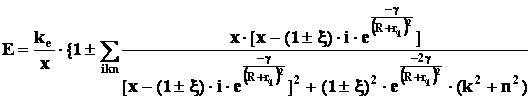   (2)

 

 

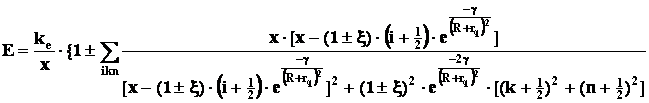
(2’)

 

Аппроксимацию зависимостей (2) и (2’) с достаточно хорошим приближением, при расстояниях r > 2d₁, можно представить в виде:

 

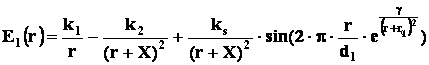          (3)

 

    где   r – расстояние  от  центрального  заряда;

d₁ – расстояние  между  центрами  осцилляторов невозбужденного вакуума;

k₁ = q*q₁/4πε_о =e²/4πε_о =2.304*10^-28 Дж ^. м = 1.44* 10^-9 эВ м (для зарядов равных е);

k₂ = k₁* r_b (из  условия  r = r_b, т.е. полная энергия E=0);

r_b – радиус орбиты первого присоединенного заряда (радиус боровской орбиты);

k_s – коэффициент  при  синусоидальной  составляющей;

X – коэффициент  описывающий  нелинейность  поляризации  вакуума;

γ – коэффициент смещения осцилляторов;

r_q– размеры частиц.

 

            Анализируя процессы, происходящие под воздействием  электростатического поля такого вида, становится понятно, что повышение частоты излучаемых фотонов происходит не только из-за увеличения энергетического уровня, но и, благодаря тому, что уменьшается параметр вакуума (расстояния между центрами осцилляторов). Иными словами, можно сказать, что при переходе от одного стационарного энергетического уровня к другому, происходит не только изменение высоты энергетического барьера, но изменяется и его ширина, и, если так можно выразится, его пространственная “крутизна”–  т.е. скорость изменения  уровня энергии на единицу расстояния, а это напрямую воздействует на частоту фотонов, излучаемых частицами.

            Таким образом, основная идея квантовой механики, о заполненности всего пространства квантовыми осцилляторами и привычная электростатика могут совместно объяснить многие свойства атомов, без привлечения волновых свойств частиц и уравнний Шредингера. Да и сами волновые свойства частиц лишь результат их движения в псевдокристаллическом вакууме.

            Приведу еще один логический пример использования  квантовой механики (КМ). В КМ существует идея “самофокусировки частиц”, в применимости к электростатическому подходу это будет выглядеть таким образом: частица, находящаяся в вакууме окружена осцилляторами, которые экранируют ее заряд, создавая, назовем его так – виртуальный заряд противоположного знака.

Попробуем, мысленно, ускорить такую систему с помощью внешнего электростатического поля. Под его воздействием сразу же произойдет некоторое разделение реального и виртуального зарядов. Т.е. возникнет диполь и сила притяжения к виртуальному заряду, направленная против воздействия поля и тормозящая, естественно, реальный заряд.

Пока скорость движения частицы невелика, по сравнению со скоростью распространения света, влияние виртуального заряда невелико, т.к. по мере движения частицы волна поляризации “успевает перестроить вакуум”.

Но вот скорость движения реального заряда приближается к скорости света, а лучше даже немного превышает ее (в диэлектриках, как мы знаем это возможно, пример тому эффект Вавилова – Черенкова). Размер диполя и отстающий виртуальный заряд резко увеличиваются, что вызывает резкий рост тормозящей силы, а это эквивалентно увеличению массы частицы.

Таким образом, становится понятен сам процесс накопления энергии движущимися частицами и телами, а так же резкое увеличение массы при приближении скорости движения к скорости света.

 

Часть III.

 

О возможности “холодного” синтеза.

 

Попробуем  с  помощью  формулы (3) решить  стандартную  задачу  взаимодействия  двух тел [6],  а  заодно  разберемся  с  коэффициентами  в  аналитической  формуле.

В  самом  общем  случае  задача  формулируется  так:  необходимо  описать  возможные  виды  движения  двух  тел,  если  известно,  какие  силы  действуют  между  ними.

Будем  считать,  что  масса  одного  тела – М  во  много  раз  больше  массы  другого – m,  чтобы  движением  тяжелого  тела  можно  было  пренеб­речь.  Так  от  двух  тел  мы  перейдём  к  задаче  о  движении  одного  тела  под  действием  известной  силы.

Пусть  это  будет  сила   притяжения,  которая  убывает  об­ратно  пропор­ционально  квадрату  расстояния.  Из  знакомых  сил, по современным представлениям,  так  себя  ведут  силы  тя­готения  и  кулоновские.  Т.о.  условия  этой  задачи  вполне  определяют  взаимодействие  протона  и  электрона.

Потенциальная  энергия  взаимодействия  выражается  формулой (3). Кинетическую  энергию  тела  удобно  представить  в  виде:

 

 

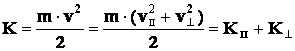
где  v_ll  и  v_^ -- составляющие  скорости  малого  тела,  направленные  по  ради­усу- вектору,  соединяющему  тела,  и  перпендикулярно  ему.  Полная  энергия  W  равна

 

W = - K_ll + K_^ + E

 

Знак  (-)  при K_ll  указывает  на  то,  что  легкое  тело  падает  на  тяжелое.  При   движении  легкого  тела  в  поле  тяжелого  со­храняется  момент  импульса

 

L = m r v_^  = const

 

тогда

K_^  = L² / 2mr²

 

Если  подставить  начальные  условия:  r равно r_n , b – прицельный  параметр,  К₀ – полная  кинетическая  энергия  (начальная),   то  можно  выразить  следую­щее  (пояснение  на  чертеже  (Фиг.5):

 

 

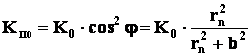
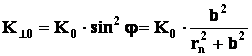
и  дополнительно  из  закона  сохранения  момента  импульса

 

 

Подставляя  все  эти  выражения  в  формулу  полной  энергии, мы  получаем:

 

 

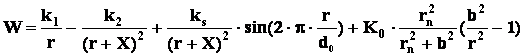
            Для упрощения расчета и большей наглядности в этой формуле мы пренебрегли экспоненциальной составляющей периода синусоиды, т.к.  принципиальной роли  изменение периода  на вид характеристики не влияет.

Необходимо  разобраться  с  коэффициентами  в  этой  формуле:

 

d_о – расстояние  между  центрами  осцилляторов;

k₁ = q*q₁/4πε_o =e²/4πε_o =2.304*10^-28 Дж ^. м = 1.44* 10^-9 эВ м

k₂ = k₁* r_b (из  условия  при  r = r_b, W=0)

 

Для  расчета  коэффициента X предположим,  что  полная  энергия  системы  равна  нулю, К₀ и  sin (2pr/d₀)  также  равны  нулю. Тогда  из  предположения,  что  мы  рассматриваем  атом  водорода  в  стационарном  состоянии

 

r = r_b = 0.53*10^-10 м

 

и  того,  что  среднеквадратичный  радиус  распределения  заряда  в  протоне

 

                                               r_s = 0.8* 10^-15 м

можем вычислить:

 

 

 

или

X² + 2rX + r² – r_br = 0

 

где  отношение  k₁/k₂  заменено  на  r_b

корни  этого  уравнения

 

 

при  r = 10^-15 м 

 X = 2.3*10^-13 м.

 

Физический  смысл  введенного  коэффициента  X  мне  пред­ставляется  как  нелинейность  поляризации  вакуумных  осцилля­торов,  но  его  величину  необходимо  уточнить,  как  и  коэффици­ент  k_s  и  их  зависимость  от  q  и  m.

Т.к.  коэффициент k_s  отвечает  только  за  образование  электронных  и  ядерных  оболочек,  мы  можем  пока  что  им пренебречь,  т.е.  приравнять  к  нулю.

Возьмем,  для  простоты  расчета,  абсолютно  точное  лобовое  столкновение   b – прицельный  параметр  приравняем  к  нулю.

Тогда  формула  полной  энергии  приобретет  вид:

 

 

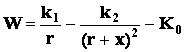
Центральный  заряд  определяет  своей  массой  искажение  вакуума,  что  и  показывает  коэффициент  k₂. Из  теории  Бора  для  водородоподобных  атомов  [4]  радиусы  стационарных  орбит  выражаются:

 

 

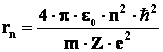
Для  первой  стационарной  орбиты  n=1

 

 

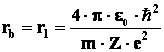
Тогда  величину  k₂  можно  выразить  в  следующем  виде:

 

 

 - постоянная  Планка;

m – приведенная  масса.

 

 

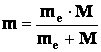
Подставляя  значение  величин,  получаем  для  протон - электронного  взаимодействия

 

 

Зная  значение  величин  коэффициентов,  можем  произвести  расчет зависимости  полной  энергии  от  расстояния.  Причем  расчет  произведем  для  пары  протон  и  позитрон, т.к.  коэффициенты  от этого  не  изменятся,  а  переход  к  более  тяжелым   частицам  не  потребует  изменения  знаков  в формуле.

По результатам  расчета  (график  (Фиг.6))  уточняем  значение  коэффициентов  k_s  и  X 

 

 

 

Строим  график  с  применением  уточненных  коэффициентов  (Фиг.7)  Из  графика  фиг.7  видно:  для  того,  чтобы  произошла  реакция  достаточно   придать  частице  кинетическую  энергию  равную  13,6  эВ.

Мы  рассмотрели  случай  лобового  столкновения,  но  для  того,  чтобы  понять  смысл  предлагаемого  способа,  необходимо  использовать  формулу  полной  энергии  взаимодействия, с помощью которой найдем сечение реакции,  фактически,  оно  определяется  прицельным  параметром  b.

 

 

Поэтому  попробуем  выразить  прицельный  параметр  через  остальные  величины.  Предположим,  что  начальное  расстояние  взаимодействия – r_н  многократно   больше   прицельного  параметра – b,  кроме  того,  выделим  вокруг  центрального  заряда  область  радиуса  r_р  при  попадании  в  которую  взаимодействующая  частица  вызовет  термоядерную  реакцию  (для  дейтерия r_р. приблизительно 1,5*10^-15 м.).  Термоядерная  реакция  произойдет,  если  полная  энергия  будет  отрицательна,  либо  равна  нулю,  при  r равном r_р.  Тогда  сечение  взаимодействия  можно  выразить  таким  образом:

 

 

Построим  график  зависимости  сечения  взаимодействия  от  кинетической  энергии  (Фиг.8).  Перерасчет  коэффициентов  по  приведенной  массе  дейтерия  дает  лишь  их  незначительное  увеличение. Например,  боровский  радиус  дейтерия

 

 

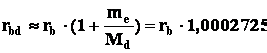
изменился  менее  чем  на  0,03 %.  При  анализе  полученного  графика,  необходимо  иметь  в  виду,  что  до  порогового  значения  кинетической  энергии  К_кр равной 13,6 эВ  будет  происходить  упругое  рассеивание  взаимодействующих  частиц.  То  же  самое  можно  сказать  и  про  частицы,  с  прицельным  параметром,  дающим  сечение  взаимодействия (при соответствующей энергии) выше  полученного  графика.

По  графику  мы  можем  определить  сечение  реакции,  при  кинетической  энергии  равной  критической  и при  энергии,  применяемой  в  современных  установках,  равной  примерно  10000 эВ.

 

 

Из  полученных  результатов  видно,  что  сечение  реакции  при  минимальной  кинетической  энергии  K_кр ,  в  615  раз  выше,  чем  при  энергиях  (≈10 кэВ) применяемых  в  современных  установках.

Рассчитаем  сечение  протон – литиевой  реакции

 

 

Из  теории  Бора  для  водородоподобных  атомов

 

 

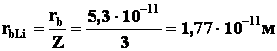
тогда

 

исходя  из  примерных  размеров  ядра  лития

 

                                              

 

  для  лития [5]                      А = 7

 

Подсчитаем  величину  X

 

 

По  величине  энергии  первого  стационарного  состояния  атома  лития,  находим  разность  энергий,  с  синусоидальной  составляющей  и  без  нее,  а  исходя  из  разности,  определяем  величину k_s.

 

∆E = E_b – E_II = 122,4 – 61,96 = 60,44 эВ

 

тогда                         

 

радиус  термоядерной  реакции, для этого случая,  равен  примерно

 

 

Подставляя  полученные  значения  коэффициентов  в  формулу  зависимости  сечения  реакции  от  кинетической  энергии,  строим  график  (Фиг.9).

 

Таким  образом,  даже  при  учете  потерь,  т.е.  при  кинетической  энергии  равной  305 эВ,  мы  получаем  двадцатикратный  выигрыш  в  вероятности  реакции,  по  сравнению  с применяемой  энергией  в 10000 эВ. Из  приведенных  примеров  можно  сделать  однозначный  вывод  о  возможности  термоядерного  синтеза  при  использовании  частиц  с  низкой  кинетической  энергией.

 

 

 

 

 

 

Часть IV.

 

Особенности термоядерных реакций протон – протонного типа.

 

 

            Исходя из выше изложенного материала может возникнуть мнение, что термоядерные реакции р – р типа должны происходить достаточно легко, чего нет на самом деле.

Рассмотрим, почему же так происходит, итак реакция (как она записана в физическом энциклопедическом словаре [1] стр. 758 табл.1):

 

 

            Т.е. данная реакция (согласно [1]) происходит с выделением энергии в 2,2 МэВ, но так ли это? Согласно закона сохранения массы – энергии имеем соотношение (данные взяты в а.е.м. из [4] т.к. они оказались наиболее усредненными)

 

 

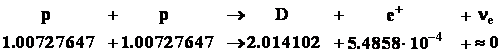
Энергетический эффект этой реакции

 

 

либо в электрон – вольтах

 

 

Таким образом, получается, что это эндоэнергетическая реакция, т.е. реакция идущая с поглощением энергии извне. Пороговая энергия данной реакции:

 

 

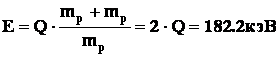
 Легко подсчитать, что температура, необходимая для протекания этой реакции должна составлять примерно 754,4 Млн.^оК. Таким образом, вероятность этой реакции даже в центре Солнца достаточно мала. В целом же, после аннигиляции позитрона, энергетический эффект реакции положителен и составляет приблизительно 0,84 МэВ.

 

 

Часть V.

 

Вакуум 2–го рода – физическая реальность.

 

            В современной физике существует множество косвенных данных, дающих основание утверждать, что вакуум 2–го рода  – реальность. Это и опыты по сканированию протонов и нейтронов электронами сверхвысоких энергий показывающие наличие их сложной структуры, составными частями которых является керн (центральное ядро),  К–  и π – мезонные оболочки. Это и излучение возбужденными ядрами γ – квантов фиксированной частоты, что явно  указывает на наличие определенных уровней энергии и возможности перехода между ними…

            Все эти данные делают правомерным предположение о том, что и вакуум 2 – го рода так же обладает определенной периодической структурой и, следовательно, к нему вполне возможно применение такого же анализа, что и к вакууму 1 – го рода проведенного во второй части статьи. Т.о. мы получим формулу для энергии электростатического взаимодействия, полностью совпадающую с формулой (3), но, естественно, со своими коэффициентами:

 

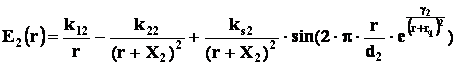      (4)

 

    где   r – расстояние  от  центрального  заряда;

d₂ – расстояние  между  центрами  осцилляторов невозбужденного вакуума 2-го

рода;

k₁₂ = q*q₁/4πε_о2;

q,q₁ – взаимодействующие заряды;

ε_о2 – диэлектрическая проницаемость вакуума 2-го рода;

r_b2 – радиус первой стационарной орбиты присоединенного заряда;

k₂₂ = k₁₂* r_b2 (из  условия  r = r_b2, т.е. полная энергия E=0 – стабильность протона);

k_s2 – коэффициент  при  синусоидальной  составляющей;

X₂ – коэффициент  описывающий  нелинейность  поляризации  вакуума 2-го рода;

γ₂ – коэффициент смещения осцилляторов;

r_q– размеры частиц.

 

Произведем приблизительную оценку параметров вакуума 2- го рода:

Исходя из того, что соотношение длин волн оптического диапазона (испускаемых атомом при возбуждении) и гамма – диапазона (испускаемых при возбуждении ядра), при учете нелинейности поляризации, составляет около 4 – 5 порядков следует что параметр вакуума 2-го рода d₂  (расстояние между центрами осцилляторов) примерно на столько же порядков меньше параметра вакуума 1-го рода. Т.к. параметр вакуума 1- го рода составляет величину равную примерно 10^-15м, то параметр вакуума 2-го рода:

 

 

Но при таких расстояниях между центрами осцилляторов, размеры самих осцилляторов должны быть еще меньше. Следовательно заряды в таких осцилляторах связаны намного прочнее и тогда, если предположить линейную  зависимость, примерно на столько же порядков уменьшится их (осцилляторов) реакция на внешнее воздействие. Т.о. вакуум 2-го рода должен обладать диэлектрической и магнитной проницаемостями примерно на столько же порядков меньшими, по сравнению  с  вакуумом 1 – го рода.

            Но тогда и скорость распространения электромагнитных взаимодействий в вакууме 2-го рода – с₂, определяемая этими величинами будет на столько же порядков выше.

 

 

Теперь, если предположить неизменной величину зарядов, можно произвести оценку коэффициентов взаимодействия:

 

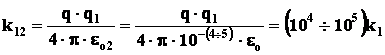
Опять же считая,  что  среднеквадратичный  радиус  распределения  заряда  в  протоне

 

                                              

 

можем вычислить:

 

где для взаимодействия зарядов по величине равных заряду электрона (с соответствующим знаком, как и в части III)

 

Определение порядка остальных коэффициентов требует более тщательного анализа, поэтому чтобы не увеличивать объема статьи не привожу.

 

Итак, получаем: полная энергия электростатического взаимодействия зарядов определяется суммарным воздействием вакуумов 1-го и 2-го родов

 

 

 

либо

 

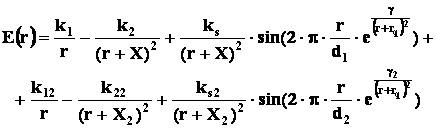        (5)

 

Анализируя график полученной функции, мы видим, что влияние вакуума 2-го рода сказывается, в основном на расстояниях равных 1÷2 d₁, и отвечает за создание “элементарных” частиц и их комплексов – ядер. При больших расстояниях влияние вакуума 2-го рода будет сказываться в виде более “высокочастотной” составляющей, накладывающейся на график функции фиг. 2 – 4. Это влияние проявляет себя в виде тонких эффектов, типа эффекта Зеемана, проявляющегося при наложении на атом внешнего магнитного поля, и некоторых других. В остальном же, анализ взаимодействия лишь в незначительных деталях отличается от анализа проведенного во второй части статьи (стр.5).

 

Итак, вакуум – двухкомпонентный диэлектрик, энергия электростатического взаимодействия в котором описывается формулой (5), представляющий собой квантовую жидкую, псевдокристаллическую, либо легко кристаллизующуюся, субстанцию.

Наиболее близким по свойствам  аналогом этого вакуума можно представить такую квантовую жидкость, как жидкий гелий.

 

 

Часть VI.

 

О невозможности существования “черных дыр”,

энергетике квазаров и “сверхновых” звезд.

 

            В этой небольшой части рассмотрим поведение вещества при сверхсильных внешних воздействиях. Начнем с момента, когда нейтронная звезда сформировалась. Но для того, чтобы произошла реакция нейтронизации, электрону должна быть сообщена энергия более чем 1,2 МэВ. Т.е. внешнее воздействие, в данном случае гравитационное, должно составлять такую величину, чтобы электрон мог преодолеть зону 3, в которой происходит, благодаря вакуумной экранировке, отталкивание зарядов противоположного знака, что обусловлено в основном воздействием вакуума 1-го рода.

            На таких расстояниях  (r ≈ 1÷2 d₁) электростатическое воздействие вакуумов 1-го и 2-го рода становятся одного порядка и, здесь возникает, небольшая по ширине, зона ядерных (частичных) оболочек. Логически рассуждая, можно прийти к выводу, что энергия притяжения должна быть немного меньше, чем 1,2 МэВ, для того, чтобы нейтрон мог распасться  на протон и электрон, при отсутствии внешнего воздействия.

            Дальше, вплоть до расстояний 1 ÷ 2 d₂ – параметров решетки вакуума 2-го рода, идет зона внутриядерного (внутринуклонного) отталкивания, т.е. зона аналогичная зоне 3 вакуума 1-го рода.

            При уровне энергии внешнего  воздействия, превышающем энергию внутриядерного отталкивания, заряды просто “аннигилируют” – т.е. преодолеют зону отталкивания и вернутся к состоянию вакуума, с выбросом, естественно, всей накопившейся энергии.

            Ударная волна, распространяясь в нейтронной звезде, вызовет цепную реакцию. Спустя некоторое время, обусловленное инерционностью вещества и накоплением достаточной кинетической энергии, остатки нейтронной звезды разлетятся, продолжая взрываться, но уже как  атомные бомбы невообразимой величины.

            Остатки непрореагировавшего вещества разлетятся в пространстве, образуя туманность. По мере остывания (потери энергии) вещество начнет вновь стягиваться  в  центр тяжести, опять, спустя некоторое время зажжется звезда, и цикл будет продолжаться.

            Итак, логически открытая, назовем ее допустим, “гравитационная” аннигиляция, и является причиной вспышек “новых” и “сверхновых”, а так же, возможно, и причиной мощного излучения квазаров.

            Т.о. незнание законов взаимодействия зарядов породило недоразумение в виде так называемых “черных дыр”, существование которых, по крайней мере, звездных размеров и меньше (размерами со Вселенную может наверное и быть) – неправомерно.

            В конце этого небольшого раздела, посвященного космологии, хотелось бы акцентировать внимание еще на одном факте: высчитывая расстояния до космических объектов, часто пользуются постоянной Хаббла – характеризуя ее как, коэффициент пропорциональности между скоростью удаления внегалактических объектов, вызванных расширением Метагалактики и расстоянием до них, вызывающей “красное” смещение  спектральных линий. Рассуждения просты: чем дальше объект, тем выше скорость его удаления, тем больше “красное” смещение спектральных линий.

            Но, как мне кажется, рассуждения ошибочны. Дело в том, что пространство, в котором распространяются фотоны не является пустотой – это вакуум. Вакуум же, как было показано выше представляет собой диэлектрик. А как бы ни хорош был этот диэлектрик, он имеет свои диэлектрическую и магнитную проницаемости. Следовательно, в нем будет наблюдаться дисперсия электромагнитного излучения. У него (вакуума) можно определить тангенс диэлектрических потерь и, следовательно, при распространении фотонов, они будут терять энергию.

            Таким образом, определять расстояние до Метагалактических объектов можно и даже нужно, а вот интерпретировать расширение Вселенной, основываясь на “красном” смещении – явная ошибка.

 

Вывод по статье:  Применение электростатического подхода, идей квантовой механики в сочетании с учетом гравитационного и магнитного взаимодействий, к исследованию строения вакуума и его свойств позволяют достаточно полно и наглядно объяснить явления широчайшего диапазона – от микромира до явлений Метагалактического масштаба.

 

 

Источники  информации  принятые  во  внимание:

 

1. Физический  энциклопедический   словарь,  гл.  редактор А.М. Прохоров,   Москва  “Большая   российская   энциклопедия” 1995 год.

            2. Курс  физики.  Т.И. Трофимова  Москва “Высшая  школа” 1998 год.

            3. Журнал  “Наука и жизнь”  №3  1980 г.  стр.32.

            4. Основы  современной  физики  В.Акоста;  К.Кован;  Б.Грэм  перевод  В.В. Толкачева.  Москва “Просвещение” 1981 г.

            5. Справочник  по  элементарной  физике  Кошкин; Ширкевич  Москва “Наука” 1976 г.

6. Как  регистрируют  частицы  А.А.Боровой  библиотечка  “КВАНТ”  выпуск  15  Москва  “Наука” 1981 г.

7. Теоретическая физика, том IV, Квантовая электродинамика  В.Б, Берестецкий, Е.М. Лившиц, Л.П. Питаевский Москва “Наука” 1989г.

8. Фейнмановские лекции по физике т.т. 8-9 Квантовая механика  Р.Фейнман, Р. Лейтон, М. Сэндс Москва “МИР” 1978 г.

9.  Космические рубежи теории относительности У. Кауфман, перевод с английского д-ра  физ.-мат. Наук, профессора Н.В. Мицкевича, Москва “МИР” 1981 г. …

 

 

09.01.05 Неделин Ф.П.