Изначальная логическая ошибка классической физики.

 

 

Математика – наука  обладающая жесткой

внутренней     логикой.    Поэтому    применяя    ее

(математику)    необходимо    строго   следить   за

точностью определений и правильной постановкой

 условий задач, анализировать каждую проделанную

операцию,   иначе   полученный   результат    будет

разительно   отличатся    от   реальности.

 

 

 

Почему возникла необходимость данной работы.

 

 

Проводя  теоретические  исследования  зависимостей  расстояния  между  объектами  от  времени  при  электрических  и  гравитационных  взаимодействиях,  мною  были  обнаружены  некоторые  нарушения  в  логических  и  математических  построениях  классических  теорий  выше  названных  процессов. Приведу некоторые из них:

1) Логическое Противоречие, возникающее при взаимодействии зарядов. Суть его можно выразить так: любая система может совершить работу, если она обладает избытком какого-либо вида энергии, будь-то потенциальной, кинетической, электростатической, тепловой, химической и т.д.

Система из двух неподвижных зарядов ОДНОГО знака, расположенных на бесконечно большом расстоянии НЕ МОЖЕТ самостоятельно произвести работы.

И напротив: Система из двух неподвижных зарядов РАЗНОГО знака, расположенных на бесконечно большом расстоянии – МОЖЕТ самостоятельно произвести работу.

Полная энергия системы, как сумма потенциальной и кинетической энергий,  по современным представлениям, и в одном, и в другом случае равны нулю.

НО каким образом система двух зарядов, полная энергия взаимодействия которой равна нулю, может произвести работу?

Более явно, как мне кажется, логика этого противоречия просматривается с другой стороны:  Система из двух зарядов Одного знака, расположенных на некотором расстоянии, стремиться самостоятельно увеличить свои размеры, т.к. обладает положительной потенциальной энергией.

Для увеличения же размеров системы двух зарядов Разного знака, мы вынуждены вносить в нее энергию извне, которая преобразуется в отрицательную потенциальную энергию этой системы.

Тогда на бесконечно большом расстоянии, система из двух зарядов Разного знака должна обладать Отрицательной потенциальной энергией, а не нулевой, как принято;

2) Это же, как следствие из закона сохранения энергии, но уже для любых систем: если система самопроизвольно совершает работу – на это расходуется запасенная в ней потенциальная энергия, которая может быть как положительной, так и отрицательной.

НО тогда: если мы совершаем работу над системой против внутренних сил системы – происходит увеличение ее (системы) внутренней потенциальной энергии (положительной или отрицательной).

Т.е. совершая работу (против внутренних сил)  над системой в которой  действуют силы притяжения, т.е. в системе действует отрицательная потенциальная энергия, мы – увеличиваем Отрицательную потенциальную энергию – ее модуль растет.

Например – растянутая пружина представляет собой такую систему, и накапливаемая в ней потенциальная энергия должна быть, по логике – Отрицательной, но в современном понимании потенциальная энергия растянутой пружины принята – положительной…

Таким образом, как только при исследовании мы сталкиваемся с системами, в которых действуют силы притяжения, сразу же возникает явное, либо неявное противоречие в логике поведения этой системы.

 

            Проведя ретроспективный анализ, в поисках причины возникновения этого логического несоответствия, установлено следующее:

            Причиной этого несоответствия  является логическая ошибка, допущенная при выводе из уравнения Лагранжа уравнения Ньютона – выражение силы, как минус производная потенциальной энергии по расстоянию.

Так это сделано, например, в книге “Теоретическая физика” Л.Д. Ландау, Е. М. Лившиц т.1 Механика Москва “Наука” главная редакция физико-математической литературы 1988 г. {в дальнейшем  [1]} стр. 18-19

 

 

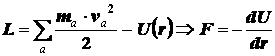
НО потенциальная энергия может иметь и другой знак, при подстановке ее (энергии) в уравнение Лагранжа получим:

 

 

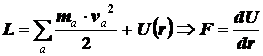
Несколько преобразуем формулы Ньютона, чтобы яснее разобраться в их смысле:

 

  при  

 

    при   

 

Но произведение силы на элемент расстояния есть элемент работы этой силы:

 

 

Тогда

  при  

 

        при   

 

Т.е. полученные выражения утверждают следующее:

- изменение положительной потенциальной энергии Противоположно по Знаку работе внутренних сил - отталкивания;

- изменение отрицательной потенциальной энергии Равно работе внутренних сил, в данном случае - притяжения.

Тогда, зависимость потенциальной энергии от расстояния, для произвольных систем можно выразить следующим образом:

 

    при    

 

    при    

 

 

где U_n – начальная потенциальная энергия системы;

       А – работа внутренних сил при изменении размеров системы.

 

Итак: Вышеобозначенная логическая ошибка привела к тому, что для различных по знаку полей были сделаны одинаковые, но неверные по сути, дальнейшие логические построения и выводы.  Весь курс теоретической физики, рассматриваемый в современных учебниках, в достаточной степени верен и справедлив для положительных потенциальных полей (для сил отталкивания), но стоит только обратиться к отрицательным полям (силам притяжения), картина резко меняется.

 

Глава 1.  Силы  взаимодействия и соответствующие им энергии.

 

            Приступая к работе необходимо уточнить и понять, что же такое  энергия и потенциальная (внутренняя) энергия системы, итак:

 

По определению в Физическом энциклопедическом словаре: ЭНЕРГИЯ (греч. – действие, деятельность) – ОБЩАЯ количественная мера ДВИЖЕНИЯ и ВЗАИМОДЕЙСТВИЯ всех видов материи. Энергия не может возникнуть из ничего и не исчезает, она может переходить из одной формы в другую (закон сохранения энергии). Понятие Энергия связывает воедино все явления природы…

 

Начнем с того, что НЕВОЗМОЖНО представить понятий скорости и силы без системы координат, хотя бы одномерной. НО тогда и понятие ЭНЕРГИЯ неразрывно связано с этой системой, ее существованием. Уберите систему – понятие ЭНЕРГИЯ теряет смысл.

Это интуитивно понятно, т. к. никакого физического интереса не представляет одиночное, ни с чем не взаимодействующее тело (заряд).

Таким образом, логика  понятия Энергия содержит в себе существование системы отсчета и, следовательно, существование как минимум двух тел в системе взаимодействия (пускай  даже  одно из  них,  скажем  так, “виртуальное” –  начало  координат  либо, так называемый, пробный заряд, это если начало координат совмещено с  воздействующим зарядом).

Следовательно, ТОЛЬКО наличие СИСТЕМЫ тел либо зарядов (как минимум двух) определяет энергию – ЭНЕРГИЮ СИСТЕМЫ этих тел (зарядов), и, следовательно, необходимо работать с этим понятием, а не просто – Энергия”.

Подчеркиваю - ЭНЕРГИЯ СИСТЕМЫ тел, а не просто энергия неизвестно к чему “привязанная”.

 

Если рассматривать простейший случай – одномерную систему, т.е. систему из двух радиально взаимодействующих частиц (тел, точек системы…), мы установим, что у нее есть только три возможности:

а) – не изменять размеров;

б) -  увеличить размер;

в) – уменьшить размер.

Все это, естественно, связано с процессами внутри самой системы (скоростью тел и силами взаимодействия).

            Случай а) – система не может изменить своих размеров. Тогда либо тела неподвижны и не взаимодействуют между собой (что явно не интересно), либо сумма всех сил, действующих на тела системы, равна нулю (пружина, сжата и затянута, допустим, ниткой; спутник на круговой орбите; тело на поверхности планеты…) – такая система не может без внешнего вмешательства измениться –  Энергия Системы равна нулю.

            Случай б) – система может увеличить свои размеры самопроизвольно – совершить работу  “наружу”- Энергия Системы - положительная (сжатая пружина, после того как мы обрезали нитку; два заряда одного знака, находящиеся на определенном расстоянии; сжатый в цилиндре (сосуде) газ…).

            Случай в) – система стремится уменьшить свои размеры –  Энергия Системы - отрицательная (растянутая и отпущенная пружина; два гравитационно  взаимодействующих  тела, либо два заряда разных знаков, разведенных на определенное расстояние и освобожденных….)

 

            Система из двух тел обладает положительной потенциальной энергией, если она стремится к самопроизвольному расширению (совершает работу вовне, без всякого внешнего воздействия). И наоборот – обладает отрицательной потенциальной энергией, если стремится сжаться (совершить работу внутрь).

 

Аналогичный проводится анализ систем с большим числом измерений, естественно при некотором усложнении, но суть остается той же…

Может возникнуть вопрос, а как же со всем этим связана Кинетическая энергия?

 

Кинетическая энергия, естественно, включается в полную энергию системы. Например для одномерной системы – если скорость тела положительная (v>0), то  кинетическая энергия войдет в формулу  Энергии Системы с положительным значением (+) К, если скорость отрицательная (v<0) – то с отрицательным значением (-) К.

            Для систем с большим числом измерений уже необходимо различать радиальную и тангенциальную составляющие полной скорости. Причем, радиальная составляющая будет входить в Энергию Системы точно так же, как и в одномерном случае, а тангенциальная составляющая (создающая положительную центробежную силу) со знаком (+).

 

            При решении определенных задач, мы этим принципами пользуемся, причем в большей степени чисто интуитивно, а здесь скрыта очень важная вещь:

 

И кинетическая энергия, и энергия гравитационного и электростатического взаимодействий связаны с изменением размеров систем, посредством сил и скоростей, а, следовательно, это суть ВЕКТОРНЫЕ величины.

 

Вот поэтому электростатические поля отталкивания (взаимодействие зарядов одного знака) учитываются как положительные – т.к. силы и энергии соответствующие этим полям стремятся увеличить размеры системы. Гравитационные и электростатические поля притяжения (взаимодействие зарядов разного знака) учитываются как отрицательные – т.к. силы и энергии соответствующие этим полям стремятся уменьшить размер системы.

Это, практически, следствие проекции соответствующих векторов на ось “расстояний” системы, отсюда у различных видов взаимодействия различные знаки.

 

Еще хотелось бы обратить ваше внимание на то, что силы, соответствующие гравитационным и электростатическим полям, направлены так, что математически, можно сказать даже арифметически, стремятся уменьшить потенциал (его модуль) соответствующего им поля.

Или по другому – силы соответствующие гравитационным и электростатическим полям, стремятся вытолкнуть тело (заряд) в область, где потенциальная энергия этого вида взаимодействия равна нулю (практически направление вектора силы указывает где нулевой потенциал поля).

 

Приведу вашему вниманию два определения, вытекающих из выше сказанного:

 

1) ПОЛНАЯ  ЭНЕРГИЯ  СИСТЕМЫ есть сумма всех энергий взаимодействия, с соответствующими знаками.

2) Модуль ПОЛНОЙ  ЭНЕРГИИ  СИСТЕМЫ, равный сумме модулей всех энергий взаимодействия, есть величина постоянная.

 

Конечно, и само собой разумеется, второе определение – закон сохранения Модуля Полной Энергии действует только для замкнутых систем.

 

                Современная физика изучает два типа сил: притяжения (отрицательные) и отталкивания (положительные). Рассмотрим работу, производимую постоянными по величине, но различными по типу, а соответственно и по знаку силами.

 

       

 

            Работа, совершаемая под действием сил, определяется интегралом следующего вида:

 

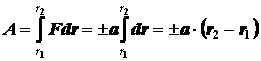
если силы положительные – а>0, то

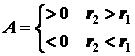
если силы отрицательные – a<0, то

 

 

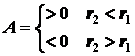
Или просто словами: при увеличении расстояния работа положительных сил – положительна, а отрицательных – отрицательна, при уменьшении расстояния – зависимости противоположные.

            Точно такие же знаки будет иметь работа, совершаемая силами, изменяющимися по величине от расстояния. Для проверки этого утверждения рассмотрим, как изменяется потенциальная энергия систем при наличии различных по типу сил.

 

1.1  Имеется пружина в виде плоской спирали (Рис.1). Найти закон изменения потенциальной энергии системы, если закон изменения силы F= - kr, где k – жесткость пружины.

            В первоначальном  состоянии, при r =0,  потенциальная  энергия  системы  пружина – подвеска равна нулю, т.к. система не может совершить никакой работы.

            Выразим работу, совершаемую пружиной при изменении расстояния, под внешним воздействием:

 

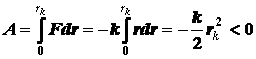
            При снятии внешнего воздействия система будет стремиться вернуться к исходному состоянию (сжаться). Следовательно, потенциальная энергия системы отрицательна и равна сумме начальной энергии системы и работе, совершаемой пружиной, при изменении расстояния от 0 до r_k.

 

либо при произвольном  r:

 

 

Выводы из рассмотренной задачи (предварительные):

            а) в системах, где действуют силы притяжения (отрицательные) потенциальная энергия – отрицательна, и ее модуль увеличивается с увеличением расстояния от точки равновесия (нуля потенциальной энергии);

            б) силы, возникающие в системах с отрицательной потенциальной энергией, стремятся вернуть систему в состояние равновесия, т.е. к нулевому значению этой потенциальной энергии.

 

Эти выводы должны быть абсолютно верны и для других систем, в которых действуют силы притяжения и обладающих отрицательной потенциальной энергией, независимо от закона изменения этих величин.

 

            1.2. Проверим это утверждение решением задачи об изменении потенциальной энергии гравитационного поля:

            Два тела массами M и m, находятся на начальном расстоянии r_n. Как изменится потенциальная энергия системы при изменении расстояния до величины r_k.

 

Начальная потенциальная энергия системы отрицательна и равна:

 

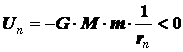
где  G – универсальная гравитационная постоянная.

Воспользуемся законом Ньютона. Тогда работу силы можно выразить с помощью интеграла следующего вида:

 

 

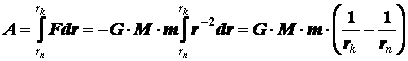
таким образом, при увеличении расстояния работа гравитационных сил – отрицательна, а при уменьшении – положительна. Т.е. такая же тенденция, что и для отрицательных сил в задаче, рассмотренной первой

 

 

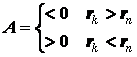
Для более четкого понимания несколько преобразуем формулу работы, прибавим и отнимем некоторую постоянную величину С.

 

 

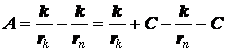
где

 

тогда работу можно выразить как разность потенциалов

 

 

где

   

 

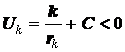
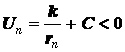
Но потенциальная энергия гравитационного поля принята отрицательной, следовательно, чтобы работа гравитационного поля была отрицательной, модуль U_k должен быть больше модуля U_n.

 

 

Тот же результат получается при выражении потенциальной энергии поля при помощи неопределенного интеграла силы

 

 

 

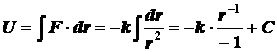
из того, что гравитационное поле – отрицательно, следует

 

                       

 

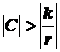
Заменив знак при С, можем записать

 

         где      

 

Итак, для силы, пропорциональной (- 1/r²), математически получена убывающая функция, которая стремится к некоторой отрицательной постоянной, при стремлении расстояния к бесконечности

 

 

 

            Так как потенциал начальной точки r_n – отрицателен, при росте расстояния работа, совершаемая силой притяжения, отрицательна, следовательно, потенциальная энергия должна убывать. В пределе, при стремлении расстояния к бесконечности, потенциал стремиться к величине – С.

Потенциальная энергия, опять же, представляет собой сумму начальной энергии системы и работы, совершаемой гравитационными силами:

 

 

Подставим в это уравнение значения начальной энергии и работы, под действие силы, задавшись произвольным значением расстояния r:

 

 

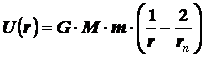
Исследование полученной зависимости показывает, что это гиперболическая функция (Рис.2), ограниченная снизу, при расстоянии стремящемся к бесконечности, величиной

 

 

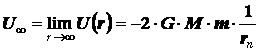
Получили, что потенциал гравитационного поля на бесконечно большом удалении фактически равен удвоенному начальному потенциалу (насколько это утверждение верно попробуем разобраться ниже).

При уменьшении начального расстояния r_n потенциальная энергия, согласно полученной формулы, устремляется к бесконечности. Это естественно неверно, т.к. гравитационное поле внутри физических тел падает, устремляясь к нулю в центре тяжести. Поэтому полученную формулу можно применять с ограничением до радиуса тела R.

 

 

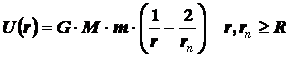
Итак, при решении данной задачи получены следующие, и довольно существенные, результаты:

а). Для сил, пропорциональных (- 1/r²), математически получена убывающая гиперболическая  функция потенциальной энергии;

б) Такое понятие, как потенциал полностью теряет смысл, т.к.  тела, находящиеся на одинаковом расстоянии от центрального тела, но имеющие различные “начальные” расстояния r_n будут иметь различные по величине потенциалы.

 

 

Рассмотренная задача подтверждает предварительные выводы из первой, перейдем к изучению следующего типа сил.

 

 

1.3. Рассмотрим задачу, в которой действуют силы отталкивания: имеется конусная пружина длинной r_о (Рис.3) с коэффициентам жесткости k. Найти выражение изменения потенциальной энергии для такой системы.

Зависимость силы от расстояния, для этого варианта:

 

 

Несжатая, свободная пружина (r = r_o) обладает нулевой потенциальной энергией, т.к. самопроизвольной работы произвести не может. И наоборот, полностью сжатая пружина способна произвести работу при расширении до размера r_o, при котором ее потенциальная энергия становится равной нулю. Таким образом, потенциальная энергия системы определяется величиной работы силы отталкивания при расширении системы от начального расстояния – r_n до полного размера пружины r_o.

 

 

 

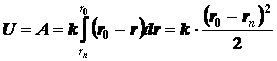
При произвольном расстоянии (r ≤ r_o) принимает вид

 

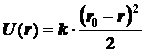  при

 

Для произвольных сил отталкивания потенциальная энергия системы представляет собой не сумму, как в случае с системами, где действуют силы притяжения, а разность начальной потенциальной энергии и работы силы при изменении расстояния.

 

 

1.4.  Рассмотрим теперь, как изменяется работа и  потенциальная энергия системы при изменении размеров такой пружины от расстояния  с нулевой энергией r_o до произвольного r_k.

 

 

 

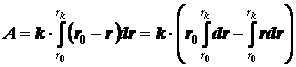
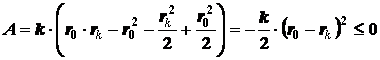
Получается, и впрочем достаточно логично, что при сжатии работа пружины отрицательна (сила – положительна, расстояние – убывает).  Но и при растяжении пружина совершает отрицательную работу, что было показано в предыдущих примерах и получено в данной формуле. Итак, при произвольном изменении расстояния r, под воздействием  внешних  сил, работа пружины – отрицательна (если пружина производит сама работу, то она (работа) положительна и при самопроизвольном сжатии, и при расширении)

 

 

Потенциальная энергия системы будет изменяться следующим образом: при растяжении пружины – будет становиться все большей по модулю, но отрицательной; при сжатии пружины – все большей по модулю, но положительной.

 

 

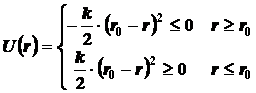
Для лучшего понимания исследуем эту задачу более подробно, в динамике, для чего построим Фазовую Энергетическую Характеристику  (ФЭХ)– зависимость изменения различных видов энергии системы от расстояния  - рис. 4

 

На графике Рис.4 изображены:

 

1) зависимость силы F(r) от изменения размеров системы (от деформации пружины) – красная наклонная линия;

2) зависимость потенциальной энергии - U(r) – фиолетовая кривая;

3) Циклическая зависимость кинетической энергии К от размеров системы: зеленым цветом - К для системы без потерь энергии (что-то напоминающее эллипс); коричневым цветом – К” для системы с потерями (“эллипсная спираль”).

 

Точки:

r0 – точка нулевой деформации – соответствует нулю потенциальной энергии системы;

r1 – точка максимального сжатия – соответствует максимальной Положительной потенциальной энергии;

r2 – точка максимального растяжения пружины – соответствует максимальной Отрицательной потенциальной энергии;

X – произвольно выбранная точка.

 

Зеленые и коричневые стрелки показывают “направление потока” энергии системы.

Движение по зеленому эллипсу, в направлении стрелок, покажет, как будет вести себя система, изменятся ее размеры, как будут взаимодействовать энергии при колебательном процессе без потерь.

            Приведенная часть коричневой “эллипсной спирали”, показывает, как будет происходить процесс затухающего колебания при наличии потерь в системе (процесс начинается из точки максимального растяжения пружины).

Произвольна точка X - показывает, что любой координате системы (за исключением, естественно, двух особых точек r1 и r2, в которых кинетическая энергия ноль)  соответствует два одинаковых по модулю, но противоположных по знаку значения Кинетической энергии. И, по-моему, это естественно, т.к. система может находиться в одном из двух состояний – сжиматься либо расширяться. Этим процессам соответствуют отрицательные и положительные скорости тел системы, и, соответственно, Отрицательные и Положительные значения Кинетической энергии.

 

 

При внешнем воздействии на систему мы выводим ее из состояния равновесия (в ту либо иную сторону). Система, с помощью присущих ей внутренних сил, стремится восстановить равновесие (восстанавливает нулевое значение полной энергии), или хотя бы сделать равным нулю значение своей потенциальной энергии.

 

            Итак:  Растяжение (помним, что исходное состояние – энергия системы ноль):

Прикладываем к пружине внешнюю силу, пружина начинает деформироваться, расстояние растет, сила сопротивления пружины (отрицательная) растет. Когда сила сопротивления пружины (отрицательная) сравнивается по величине с внешней силой (положительной), система приходит в равновесие.

Работа внешней, положительной, силы при увеличении расстояние – положительная, работа внутренней силы (отрицательной) при увеличении расстояния – отрицательная.

Величины этих работ равны по величине и противоположны по знаку – в сумме дают ноль – т.о. система пришла к новому состоянию равновесия с Нулевой энергией.

 

Закон сохранения энергии нарушен? – Нет.         НО в системе накоплена Отрицательная потенциальная энергия, которая компенсирует внешнюю (положительную), и стоит снять внешнее воздействие, система опять будет стремиться восстановить равновесие, т.е. достичь  нулевого значения полной энергии или, как я уже писал, хотя бы нулевого значения потенциальной энергии.

 

Как это происходит? Фаза первая: Снимаем внешнюю силу.  НО в пружине накоплена Отрицательная потенциальная энергия (деформации), следовательно, действует сила притяжения (отрицательная) – пружина начинает сжиматься. Сила – отрицательная, расстояние – уменьшается, следовательно, Работа, совершаемая пружиной – положительная (потенциальная энергия при этом стремится к нулю). Концу пружины (всей пружине и грузу (телу)) сообщается отрицательная кинетическая энергия (т.к. скорость отрицательная). При достижении точки равновесия r0 (нулевая деформация – начальное расстояние) – бывшая отрицательная потенциальная энергия системы равна нулю, ибо полностью перешла в Отрицательную Кинетическую энергию пружины и груза (тела).

 

Закон Сохранения Энергии нарушен – Нет! Вплоть до знаков все верно!

 

Деформация пружины равна нулю (потенциальная энергия – ноль), а кинетическая энергия достигла своего максимального ОТРИЦАТЕЛЬНОГО  значения.

НО теперь уже необходимо учитывать, что пружина деформируется в другую сторону – возникает сила сопротивления сжатию – ПОЛОЖИТЕЛЬНАЯ.

Здесь и начинает сказываться Различие между взаимодействиями в полях Положительных и Отрицательных сил.

 

Итак, рассматриваем дальше, очередная - вторая фаза:

Начальный потенциал данной фазы U_о = 0; кинетическая энергия К = - (К_о) - отрицательна и равна по модулю внесенной внешней силой энергии на фазе растяжения.

Отрицательная Кинетическая энергия  эквивалентна тому, что на систему воздействует внешняя Отрицательная сила (сжимающая систему), которая при уменьшении расстояния (размеров) – совершает над системой Положительную работу. Т.е. полная аналогия воздействия внешних сил (примем индексом для внешних сил и всего что к ним относится малую латинскую  v). Тогда

 

 

где Av –  работа внешних сил;

К_о – кинетическая энергия подвижного тела системы в начальный момент данной фазы; Fv – эквивалентная внешняя сила (Отрицательная);

r_о; r – “начальный” и “конечный” размер системы.

Работа внутренней силы системы (сила положительна, расстояние убывает) отрицательна и численно равна Кинетической энергии. При учете того, что начальный потенциал ноль, получаем:

 

 

Т.о. кинетическая энергия полностью преобразовалась в Положительную Потенциальную энергию сжатой пружины.

Следующая третья фаза: Начальный потенциал системы равен U_о = K_о (модуль начальной кинетической энергии), Кинетическая энергия системы (точка крепления - пружины + тело) равна нулю. Сдерживающей силы нет (в этом отличие), следовательно, пружина начинает разжиматься. Что же получится, когда пружина полностью отпущена (в точке нулевой деформации)?

            Работа, совершаемая внутренними силами – Положительная (т.к. сила Положительная и расстояние растет) и опять же, при отсутствии потерь, равна А = U_о = К_о.

Тогда потенциальная энергия системы, согласно выше приведенной формулы:

 

 

Затем следующая фаза, ну и так далее…

 

            Итак, исследование систем со знакопеременными силами приводит к следующим выводам:

1. Силы, возникающие в системах со знакопеременными полями, стремятся вернуть систему в состояние равновесия, т.е. к нулевому значению потенциальной энергии системы.

Иными словами: все тела стремятся не к минимуму потенциальной энергии, как это трактуется в современной физике, а к ее нулю. Если потенциальная энергия системы – положительна, то силы положительные, система стремится расшириться. И наоборот, потенциальная энергия системы – отрицательна, то силы отрицательны, система стремится сжаться.

2. Если система находится в состоянии равновесия, то ее полная потенциальная энергия равна  нулю, воздействие любых сил взаимоскомпенсировано, т.е. сумма сил, действующих  на тела, так же равна нулю.

Иными словами: если размеры системы не изменяются, то она находится в состоянии равновесия и сумма сил, воздействующих на тела системы, равна нулю, как и ее потенциальная энергия. Например: тела, лежащие на поверхности Земли, плавающие, вращающиеся по круговым орбитам и т.д.

 

Итак, решив эти несколько задач и пользуясь только простейшими логикой и математикой мы получили результаты, кардинально отличающиеся от принятых современной физикой.

 

1.5   Рассмотрим  калибровку в ноль на бесконечно большом расстоянии:

 

а)  Итак, для положительных полей анализ не изменяется

 

 

При подстановке зависимости силы от расстояния k/r² получим

 

       

 

В этом случае признание равенства нулю, на бесконечно большом расстоянии, потенциальной энергии – логично и абсолютно оправдано. Следовательно, вполне правомерно признать равной нулю постоянную интегрирования С, тогда формула принимает стандартный вид:

 

б) При анализе отрицательных  полей в классическом варианте получим следующее:

 

 

при калибровке в ноль на бесконечно большом расстоянии (С=0)

 

 

но тогда работа отрицательного поля, выраженная через разность потенциалов, при увеличении расстояния (r_k  > r_n) получается положительной (!!!)

 

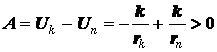     при 

 

что, конечно же, неестественно, не может отрицательная сила при увеличении расстояния совершить положительную  работу (задача 1.2  стр.6).

            Для отрицательных полей

 

 

изменяет интеграл и при подстановке зависимости -k/r² получаем (как и во второй задаче)

 

    тогда         

 

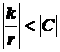
либо приняв постоянную С больше нуля

 

  (при С ≥ 0)

 

Но тогда при калибровке в ноль на бесконечности, т.е. при присвоении нулю постоянной С получим функцию неотличимую от предыдущей

 

 

 

что естественно неверно. Как было показано при решении второй задачи (1.2 стр.8), потенциал отрицательных полей на бесконечно большом удалении получается равным удвоенному начальному потенциалу.

 

 

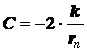
            Таким образом, отрицательные поля должны калиброваться в ноль не при бесконечно большом удалении, а наоборот при стремлении к нулю расстояния между телами.

 

            Итак, прежде чем переходить к следующей части работы, повторим основные выводы этой главы:

 

           1.  В системах, где действуют силы притяжения (отрицательные) потенциальная энергия – отрицательна, и ее модуль увеличивается с увеличением расстояния от точки равновесия (нуля потенциальной энергии);

2.  Силы, возникающие в системах со знакопеременными полями, стремятся вернуть систему в состояние равновесия, т.е. к нулевому значению потенциальной энергии системы;

3. Если система находится в состоянии равновесия, то ее полная потенциальная энергия равна  нулю, воздействие любых сил взаимоскомпенсировано, т.е. сумма сил, действующих  на тела, так же равна нулю.

4.   Для сил, пропорциональных (- 1/r²), математически получена убывающая гиперболическая  функция потенциальной энергии;

5.  Такое понятие, как потенциал полностью теряет смысл, т.к.  тела, находящиеся на одинаковом расстоянии от центрального тела, но имеющие различные “начальные” расстояния r_n будут иметь различные по величине потенциалы.